Approche mathématique peut prédire la structure cristalline en quelques heures au lieu de mois

14 novembre 2024

Cet article a été examiné selon le processus éditorial et les politiques de Science X. Les éditeurs ont mis en évidence les attributs suivants tout en veillant à la crédibilité du contenu :

vérification des faits

publication évaluée par des pairs

source de confiance

corrigé par Rachel Harrison, Université de New York

Des chercheurs de l'Université de New York ont mis au point une approche mathématique pour prédire les structures de cristaux - une étape critique dans le développement de nombreux médicaments et appareils électroniques - en quelques heures seulement en utilisant un ordinateur portable, un processus qui nécessitait auparavant des semaines ou des mois sur un supercalculateur. Leur nouveau cadre est publié dans la revue Nature Communications.

Les cristaux moléculaires organiques sont une classe importante de matériaux dans de nombreuses industries, des produits pharmaceutiques et de l'agriculture à l'électronique et aux explosifs. Les cristaux sont les éléments constitutifs de nombreux médicaments en vente libre et sur ordonnance, des insecticides pour lutter contre les moustiques, des explosifs comme le TNT, des semi-conducteurs et des technologies d'émission de lumière utilisées dans les écrans de télévision et les téléphones portables.

Malgré l'omniprésence des cristaux moléculaires dans de nombreux produits de la vie quotidienne, la capacité de prédire leurs structures tridimensionnelles reste un défi, surtout si un composé peut cristalliser sous différentes formes. Dans un exemple dramatique de la nécessité de prédire les structures cristallines, des scientifiques ont découvert à la fin des années 1990 que les capsules du médicament contre le VIH, le ritonavir, se transformaient plus tard de la forme cristalline connue en une forme inconnue mais plus stable. Ce changement dans la structure cristalline rendait le médicament inefficace et l'a contraint à sortir du marché jusqu'à ce qu'une nouvelle formulation soit créée.

La plupart des approches actuelles pour prédire les structures cristallines utilisent des méthodes basées sur la physique qui présentent des limitations, telles que l'introduction de biais et d'erreurs ou la prédiction de trop nombreuses formes cristallines par rapport à celles observées dans les expériences. De plus, ces méthodes nécessitent une puissance de calcul significative et peuvent prendre des semaines à des mois, selon la complexité des molécules constitutives.

"Ces approches basées sur la physique, qui sont coûteuses et qui prennent beaucoup de temps, produisent des prédictions aussi précises que la physique qu'on y intègre, c'est pourquoi il y a eu une tendance vers les méthodes de calcul qui peuvent pallier cette lacune", a déclaré Mark Tuckerman, professeur de chimie et de mathématiques à l'Université de New York et auteur principal de l'étude.

Pour relever ce défi, Tuckerman et Nikolaos Galanakis, un chercheur postdoctoral de NYU, ont développé une nouvelle approche mathématique qu'ils ont nommée "Crystal Math" pour prédire les structures cristallines en se basant sur des règles mathématiques pures régissant la façon dont les molécules s'ordonnent dans les cristaux et quelques descripteurs physiques simples de l'environnement du cristal.

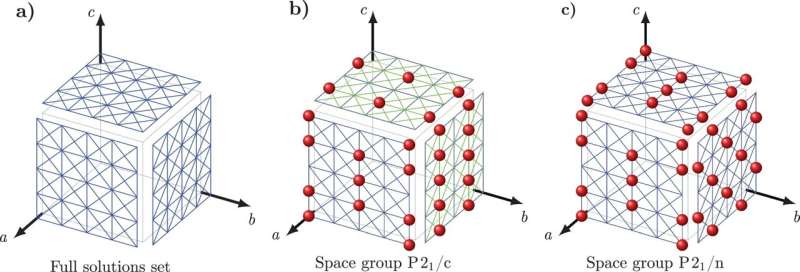
Crystal Math résout alors 13 paramètres de base liés à l'arrangement de molécules dans le cristal - y compris la position et l'orientation moléculaire et la géométrie des blocs de construction de base du cristal - ainsi que d'autres facteurs géométriques définissant la forme de chaque molécule dans le cristal.

Tuckerman et Galanakis ont vérifié les règles de Crystal Math en utilisant le Cambridge Crystal Data Centre, une base de données de centaines de milliers de structures cristallines moléculaires organiques connues. Plus précisément, les chercheurs ont vérifié si leurs règles mathématiques hypothétiques étaient respectées par les structures de la base de données, ce qui les a guidés vers des principes que les structures connues étaient très susceptibles de suivre.

Ils ont ensuite intégré ces principes dans un ensemble d'équations dont les solutions peuvent maintenant être utilisées pour prédire des structures cristallines moléculaires non présentes dans la base de données. Des médicaments courants tels que l'aspirine et le paracétamol, dont les structures sont déjà connues, ont été utilisés comme cas de test simples.

Ensuite, en utilisant les équations de Crystal Math, les chercheurs ont appliqué leur procédure à des cristaux moléculaires plus complexes, y compris des molécules hautement flexibles, dont les structures ne sont pas dans la base de données, et ont obtenu des prédictions de structure correspondant à celles générées dans des expériences avec une grande précision.

"Nos équations semblent, pour l'instant, nous donner uniquement des structures cristallines réalisables expérimentalement, ce qui résout le problème des méthodes basées sur la physique qui ont tendance à 'surestimer' le nombre de structures possibles, ce qui signifie que certaines des structures prédites peuvent ne jamais être trouvées expérimentalement", a déclaré Tuckerman.

Importamment, les solutions peuvent être obtenues en quelques heures seulement sur un ordinateur portable standard, sans nécessiter les échelles de temps longues et les ordinateurs haute performance requis par les méthodes basées sur la physique.

"Le temps de solution n'est plus de semaines à des mois - nous pouvons obtenir une solution une nuit car résoudre les équations est relativement rapide", a ajouté Tuckerman.

Crystal Math représente l'aboutissement de sept années de travail de Tuckerman et Galanakis pour concevoir une solution mathématique à ce problème de grand défi. Tuckerman a été particulièrement inspiré par un article de 1967 du mathématicien suisse et cristallographe Johann Jakob Burckhardt, qui suggérait qu'il devrait être possible d'utiliser les mathématiques pour prédire les structures cristallines, sans proposer de solution propre.

Plus de 55 ans plus tard, le protocole mathématique basé sur les travaux de Tuckerman et Galanakis a suscité l'intérêt de l'industrie pharmaceutique et présente des promesses pour l'investigation de composés encore à découvrir et pour la prédiction de leurs structures cristallines.

"La capacité même de développer de nouveaux produits repose sur le fait de savoir si les composés qui les constituent vont cristalliser, combien de formes cristallines sont possibles et la stabilité de ces différentes formes," a déclaré Tuckerman. "Avec notre approche mathématique, il est possible de tester la capacité de nombreux composés à cristalliser et de déterminer si ces structures sont adaptées à une mise sur le marché ultime."

Plus d'informations: Nikolaos Galanakis et al, Prédiction rapide des structures cristallines moléculaires en utilisant des descripteurs topologiques et physiques simples, Nature Communications (2024). DOI: 10.1038/s41467-024-53596-5

Informations sur la revue: Nature Communications

Fourni par Université de New York