Enfoque matemático puede predecir la estructura cristalina en horas en lugar de meses

14 de noviembre de 2024

Este artículo ha sido revisado de acuerdo con el proceso editorial y las políticas de Science X. Los editores han destacado los siguientes atributos mientras aseguraban la credibilidad del contenido:

verificado por hechos

publicación revisada por pares

fuente confiable

corregido

por Rachel Harrison, Universidad de Nueva York

Investigadores de la Universidad de Nueva York han ideado un enfoque matemático para predecir las estructuras de cristales, un paso crítico en el desarrollo de muchos medicamentos y dispositivos electrónicos, en cuestión de horas utilizando solo una computadora portátil, un proceso que anteriormente requería semanas o meses en una supercomputadora. Su nuevo marco de trabajo se publica en la revista Nature Communications.

Los cristales moleculares orgánicos son una clase importante de materiales en muchas industrias, desde productos farmacéuticos y agricultura hasta electrónica y explosivos. Los cristales son los elementos básicos que componen muchos medicamentos de venta libre y con receta, insecticidas para combatir los mosquitos, explosivos como el TNT, semiconductores y tecnologías emisoras de luz utilizadas en pantallas de televisión y teléfonos celulares.

A pesar de la omnipresencia de los cristales moleculares en muchos productos de uso diario, la capacidad para predecir sus estructuras tridimensionales sigue siendo un desafío, especialmente si un compuesto puede cristalizarse en múltiples formas. En un ejemplo dramático de la necesidad de predecir las estructuras cristalinas, los científicos a finales de la década de 1990 descubrieron que las cápsulas del medicamento contra el VIH ritonavir se transformaron posteriormente de la forma cristalina conocida en una forma desconocida pero más estable. Este cambio en la estructura cristalina volvió ineficaz al fármaco y lo sacó del mercado hasta que se creó una nueva formulación.

La mayoría de los enfoques actuales para predecir estructuras cristalinas utilizan métodos basados en la física que tienen limitaciones, incluyendo la introducción de sesgos y errores o la predicción de demasiadas formas de cristal de las que realmente ocurren en los experimentos. Además, los métodos requieren una potencia informática significativa y pueden tardar semanas o meses, dependiendo de la complejidad de las moléculas constituyentes.

'Estos enfoques basados en la física, que son costosos y consumen mucho tiempo, producen predicciones que son tan precisas como la física que se introduce en ellos, razón por la cual ha habido un impulso hacia métodos computacionales que pueden abordar esta deficiencia', dijo Mark Tuckerman, profesor de química y matemáticas en la NYU y autor senior del estudio.

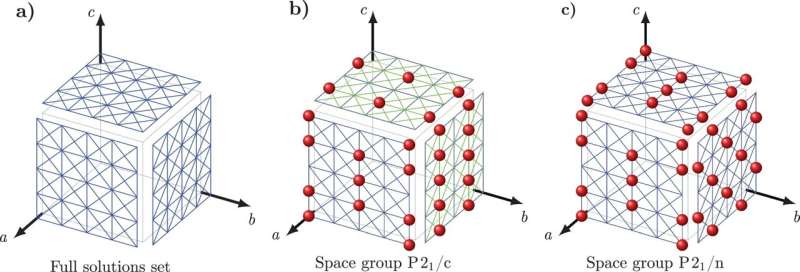
Para superar este desafío, Tuckerman y Nikolaos Galanakis, un investigador postdoctoral de la NYU, desarrollaron un nuevo enfoque matemático que han llamado 'Crystal Math' para predecir estructuras cristalinas basadas en reglas matemáticas puras que rigen cómo se empaquetan las moléculas en los cristales y algunos descriptores físicos simples del entorno del cristal.

Crystal Math luego resuelve 13 parámetros básicos relacionados con la disposición de las moléculas en el cristal, incluida la ubicación y orientación molecular y la geometría de los bloques básicos del cristal, además de otros factores geométricos que definen la forma de cada molécula en el cristal.

Tuckerman y Galanakis verificaron las reglas de Crystal Math utilizando el Cambridge Crystal Data Centre, una base de datos de cientos de miles de estructuras orgánicas moleculares cristalinas conocidas. Específicamente, los investigadores probaron si sus reglas matemáticas hipotetizadas eran obedecidas por las estructuras en la base de datos, lo que los guió hacia principios que las estructuras conocidas seguían con alta probabilidad.

Luego incorporaron estos principios en un conjunto de ecuaciones cuyas soluciones ahora se pueden utilizar para predecir estructuras cristalinas moleculares no encontradas en la base de datos. Fármacos comunes como la aspirina y el paracetamol, cuyas estructuras ya son conocidas, se utilizaron como casos de prueba simples.

A continuación, utilizando las ecuaciones de Crystal Math, los investigadores aplicaron su procedimiento a cristales moleculares más complejos, incluidas moléculas altamente flexibles, cuyas estructuras no están en la base de datos y obtuvieron predicciones de estructuras que coincidieron con las generadas en experimentos con alta precisión.

'Hasta ahora, nuestras ecuaciones parecen proporcionarnos solo estructuras cristalinas que se pueden realizar experimentalmente, lo que aborda el problema de los métodos basados en la física que tienden a 'sobrepredecir' el número de estructuras posibles, lo que significa que algunas de las estructuras predichas pueden nunca encontrarse experimentalmente', dijo Tuckerman.

Importante, las soluciones se pueden lograr en solo unas pocas horas en una computadora portátil estándar, en lugar de requerir las escalas de tiempo largas y las computadoras de alto rendimiento necesarias en los métodos basados en la física.

'El tiempo de resolución ya no es de semanas a meses, podemos obtener una solución durante la noche porque resolver las ecuaciones es relativamente rápido', agregó Tuckerman.

Crystal Math representa la culminación de siete años de trabajo de Tuckerman y Galanakis para idear una solución matemática a este gran problema desafiante. Tuckerman se inspiró particularmente en un documento de 1967 del matemático y cristalógrafo suizo Johann Jakob Burckhardt, quien sugirió que debería ser posible usar matemáticas para predecir estructuras cristalinas, pero no presentó una solución propia.

Más de 55 años después, el protocolo matemático de Tuckerman y Galanakis ha despertado interés en la industria farmacéutica y promete investigar compuestos aún no descubiertos y predecir sus estructuras cristalinas.

'La capacidad de desarrollar nuevos productos se basa en saber si los compuestos que los constituyen se cristalizarán, cuántas formas cristalinas son posibles y la estabilidad de estas formas diversas', dijo Tuckerman. 'Con nuestro enfoque matemático, es posible probar la capacidad de muchos compuestos para cristalizarse y determinar si estas estructuras son adecuadas para su despliegue final en el mercado'.

Más información: Nikolaos Galanakis et al, Predicción rápida de estructuras cristalinas moleculares utilizando descriptores topológicos y físicos simples, Comunicaciones de la Naturaleza (2024). DOI: 10.1038/s41467-024-53596-5

Información sobre la revista: Comunicaciones de la Naturaleza

Proporcionado por Universidad de Nueva York