Mathematical Method Accelerates Crystal Structure Predictions from Months to Hours

November 14, 2024

This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:

• fact-checked
• peer-reviewed publication
• trusted source
• proofread

by Rachel Harrison, New York University

Researchers at New York University have devised a mathematical approach to predict the structures of crystals—a critical step in developing many medicines and electronic devices—in a matter of hours using only a laptop, a process that previously took a supercomputer weeks or months. Their novel framework is published in the journal Nature Communications.

Organic molecular crystals are an important class of materials in many industries, from pharmaceuticals and agriculture to electronics and explosives. Crystals are the building blocks that make up many over-the-counter and prescription drugs, insecticides to fight mosquitoes, explosives such as TNT, semiconductors, and light-emitting technologies used in television screens and cell phones.

Despite the ubiquity of molecular crystals in many everyday products, the ability to predict their three-dimensional structures remains a challenge, especially if a compound can crystallize into multiple forms. In one dramatic example of the necessity of predicting crystal structures, scientists in the late 1990s discovered that capsules of the HIV drug ritonavir later transformed from the known crystal form into an unknown but more stable form. This change in crystal structure rendered the drug ineffective and forced it off the market until a new formulation was created.

Most current approaches for predicting crystal structures use physics-based methods that have limitations, including introducing bias and errors or predicting too many crystal forms than actually occur in experiments. Moreover, the methods require significant computing power and can take weeks to months, depending on the complexity of the constituent molecules.

'These physics-based approaches—which are costly and time-consuming—produce predictions that are only as accurate as the physics you put into them, which is why there has been a push toward computational methods that can address this shortcoming,' said Mark Tuckerman, professor of chemistry and mathematics at NYU and the study's senior author.

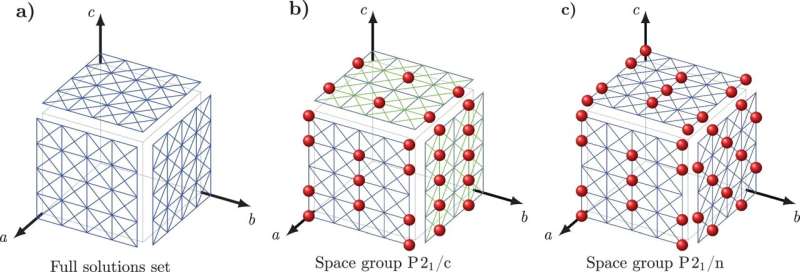
To overcome this challenge, Tuckerman and Nikolaos Galanakis, an NYU postdoctoral researcher, developed a new mathematical approach that they've named 'Crystal Math' to predict crystal structures based on purely mathematical rules governing how molecules pack into crystals and a few simple physical descriptors of the crystal's environment.

Crystal Math then solves for 13 basic parameters related to the arrangement of molecules in the crystal—including molecular location and orientation and the geometry of the crystal's basic building blocks—plus other geometric factors that define the shape of each molecule in the crystal.

Tuckerman and Galanakis verified the rules of Crystal Math using the Cambridge Crystal Data Centre, a database of hundreds of thousands of known organic molecular crystal structures. Specifically, the researchers tested whether their hypothesized mathematical rules were obeyed by the structures in the database, which guided them toward principles that known structures were highly likely to follow.

They then built these principles into a set of equations whose solutions can now be used to predict molecular crystal structures not found in the database. Common pharmaceuticals such as aspirin and paracetamol, whose structures are already known, were used as simple test cases.

Next, using the equations of Crystal Math, the researchers applied their procedure to more complex molecular crystals, including highly flexible molecules, whose structures are not in the database and obtained structure predictions that matched those generated in experiments with high accuracy.

'Our equations appear, so far, to give us only experimentally realizable crystal structures, which addresses the problem of physics-based methods that tend to 'overpredict' the number of possible structures, meaning that some of the predicted structures may never be found experimentally,' said Tuckerman.

Importantly, the solutions can be achieved in just a few hours on a standard laptop, rather than requiring the long time scales and high-performance computers required of physics-based methods.

'The time to solution is no longer weeks to months—we can get a solution overnight because solving the equations is relatively quick,' added Tuckerman.

Crystal Math represents the culmination of seven years of work by Tuckerman and Galanakis to devise a mathematical solution to this grand-challenge problem. Tuckerman was particularly inspired by a 1967 paper by Swiss mathematician and crystallographer Johann Jakob Burckhardt, who suggested that it should be possible to use math to predict crystal structures, yet didn't put forward a solution of his own.

More than 55 years later, Tuckerman and Galanakis's math-based protocol has drawn interest from the pharmaceutical industry and holds promise for investigating yet-to-be discovered compounds and predicting their crystal structures.

'The very ability to develop new products relies on knowing if the compounds that constitute them will crystallize, how many crystal forms are possible, and the stability of these various forms,' said Tuckerman. 'With our mathematical approach, it is possible to test the ability of many compounds to crystallize and determine if these structures are suitable for ultimate deployment on the market.'

More information: Nikolaos Galanakis et al, Rapid prediction of molecular crystal structures using simple topological and physical descriptors, Nature Communications (2024). DOI: 10.1038/s41467-024-53596-5

Journal information: Nature Communications

Provided by New York University