Un trucco matematico di 800 anni potrebbe aiutare nella navigazione lunare

Questo articolo è stato revisionato secondo il processo editoriale e le politiche di Science X. Gli editori hanno evidenziato i seguenti attributi assicurandone la credibilità del contenuto:

• controllo dei fatti
• fonte affidabile
• correzione di bozze

all'Università Eötvös Loránd,

Kamilla Cziráki, una studentessa di geofisica presso la Facoltà di Scienze dell'Università Eötvös Loránd (ELTE), ha adottato un nuovo approccio per studiare i sistemi di navigazione che possono essere utilizzati sulla superficie della Luna per pianificare future missioni.

Collaborando con il professor Gábor Timár, capo del Dipartimento di Geofisica e Scienze Spaziali, Cziráki ha calcolato i parametri utilizzati nel sistema GPS terrestre per la Luna utilizzando il metodo del matematico Fibonacci, che visse 800 anni fa. I risultati delle loro ricerche sono stati pubblicati sulla rivista Acta Geodaetica et Geophysica.

Ora, mentre l'umanità si prepara a ritornare sulla Luna dopo mezzo secolo, l'attenzione si concentra sui possibili metodi di navigazione lunare. È probabile che i moderni successori dei veicoli lunari delle missioni Apollo saranno assistiti da una forma di navigazione satellitare simile al sistema GPS terrestre. Nel caso della Terra, questi sistemi non tengono conto della forma effettiva del nostro pianeta, il geoide, né della superficie definita dal livello del mare, bensì di un ellissoide rotante che si avvicina meglio al geoide.

La sua intersezione è un'ellisse che è più lontana dal centro di massa della Terra all'equatore e più vicina ai poli. Il raggio della Terra è di poco meno di 6,400 chilometri, e i poli sono circa 21,5 chilometri più vicini al centro rispetto all'equatore.

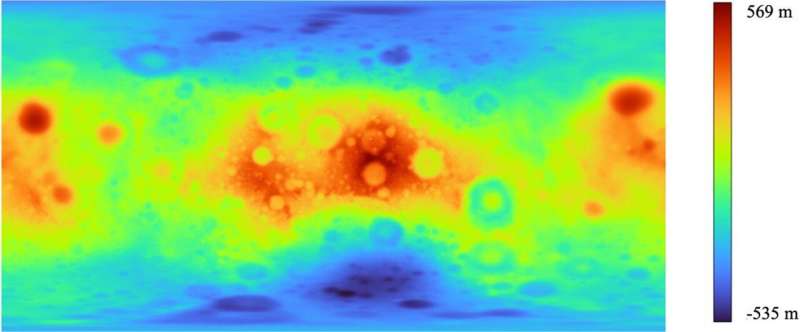
Perché la forma dell'ellissoide che si avvicina meglio alla Luna è interessante e quali parametri possono essere utilizzati per descriverla? Perché è interessante che rispetto al raggio medio della Luna di 1,737 chilometri, i suoi poli siano circa mezzo chilometro più vicini al suo centro di massa rispetto all'equatore? Se vogliamo applicare le soluzioni software testate e collaudate nel sistema GPS alla Luna, dobbiamo specificare due numeri, l'asse semimaggiore e l'asse semiminore di quest'ellissoide, in modo che i programmi possano essere facilmente trasferiti dalla Terra alla Luna.

La Luna ruota più lentamente, con un periodo di rotazione uguale al suo periodo orbitale intorno alla Terra. Questo rende la Luna più sferica. È quasi una sfera, ma non del tutto. Tuttavia, per la mappatura della Luna che è stata fatta finora, è stato sufficiente approssimare la forma a una sfera, e coloro che sono stati più interessati alla forma del nostro compagno celeste hanno utilizzato modelli più complessi.

Curiosamente, l'approssimazione della forma della Luna con un ellissoide rotante non era mai stata fatta prima. L'ultima volta che calcoli simili furono effettuati fu negli anni '60 dagli scienziati spaziali sovietici, utilizzando dati del lato della Luna visibile dalla Terra.

Cziráki, studentessa di secondo anno di geoscienze specializzata in geofisica, ha lavorato con il suo supervisore, Timár, per calcolare i parametri dell'ellissoide rotante che si avvicinava meglio alla forma teorica della Luna.

Per fare ciò, hanno utilizzato un database di una superficie di potenziale esistente, chiamata selenoide lunare, da cui hanno prelevato un campione di altezza in punti uniformemente spaziati sulla superficie e hanno cercato gli assi semimaggiori e semiminori che si avvicinavano meglio a un ellissoide rotante. Aumentando gradualmente il numero di punti di campionamento da 100 a 100,000, i valori dei due parametri si sono stabilizzati a 10,000 punti.

Uno dei passaggi principali del lavoro è stato quello di investigare come distribuire N punti uniformemente su una superficie sferica, con diverse soluzioni possibili; Cziráki e Timár hanno scelto quella più semplice, chiamata sfera di Fibonacci. La corrispondente spirale di Fibonacci può essere implementata con codice molto breve e intuitivo, e le fondamenta di questo metodo sono state gettate dall'antico matematico Leonardo Fibonacci. Il metodo è stato applicato anche alla Terra come verifica, ricostruendo una buona approssimazione dell'ellissoide WGS84 utilizzato dal GPS.

Fornito da Eötvös Loránd University