Un tour de magie mathématique vieux de 800 ans pourrait aider à la navigation lunaire.

Cet article a été examiné selon le processus éditorial et les politiques de Science X. Les éditeurs ont souligné les attributs suivants tout en veillant à la crédibilité du contenu :

• fact-checké
• source fiable
• corrigé

par l'Université Eötvös Loránd

Kamilla Cziráki, étudiante en géophysique à la Faculté des sciences de l'Université Eötvös Loránd (ELTE), a adopté une nouvelle approche pour étudier les systèmes de navigation pouvant être utilisés à la surface de la lune pour planifier de futurs voyages.

En travaillant avec le professeur Gábor Timár, responsable du département de géophysique et des sciences spatiales, Cziráki a calculé les paramètres utilisés dans le système GPS terrestre pour la lune en utilisant la méthode du mathématicien Fibonacci, qui vivait il y a 800 ans. Leurs résultats ont été publiés dans le journal Acta Geodaetica et Geophysica.

Maintenant, alors que l'humanité se prépare à retourner sur la lune après un demi-siècle, l'accent est mis sur les méthodes possibles de navigation lunaire. Il semble probable que les successeurs modernes des véhicules lunaires des missions Apollo seront désormais assistés par une forme de navigation par satellite, similaire au système GPS sur Terre. Dans le cas de la Terre, ces systèmes ne tiennent pas compte de la forme réelle de notre planète, le géoïde, ni même de la surface définie par le niveau de la mer, mais d'un ellipsoïde rotatif qui s'adapte le mieux au géoïde.

Son intersection est une ellipse qui est la plus éloignée du centre de masse de la Terre à l'équateur et la plus proche à ses pôles. Le rayon de la Terre est légèrement inférieur à 6 400 kilomètres et les pôles sont d'environ 21,5 kilomètres plus proches du centre que l'équateur.

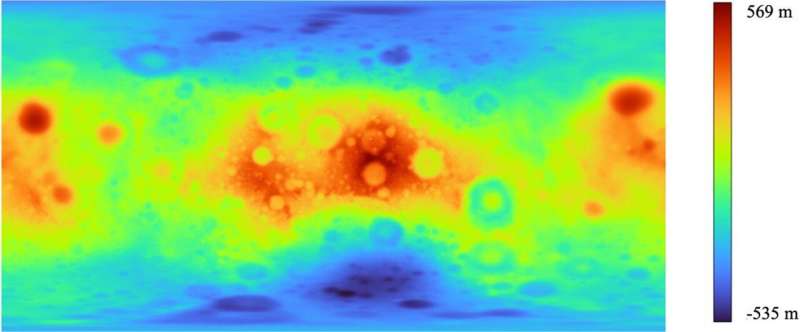
Pourquoi la forme de l'ellipsoïde qui s'adapte le mieux à la lune est-elle intéressante, et quels paramètres peuvent être utilisés pour la décrire ? Pourquoi est-il intéressant de noter que par rapport au rayon moyen de la lune de 1 737 kilomètres, ses pôles sont d'environ un demi-kilomètre plus proches de son centre de masse que son équateur ? Si nous voulons appliquer les solutions logicielles testées et éprouvées dans le système GPS à la lune, nous devons spécifier deux nombres, l'axe semi-majeur et l'axe semi-minor de cet ellipsoïde, afin que les programmes puissent être facilement transférés de la Terre à la lune.

La lune tourne plus lentement, avec une période de rotation égale à sa période orbitale autour de la Terre. Cela rend la lune plus sphérique. C'est presque une sphère, mais pas tout à fait. Néanmoins, pour la cartographie de la lune effectuée jusqu'à présent, il a été suffisant d'approximer la forme d'une sphère, et ceux qui se sont intéressés davantage à la forme de notre compagnon céleste ont utilisé des modèles plus complexes.

Curieusement, l'approximation de la forme de la lune avec un ellipsoïde rotatif n'a jamais été faite auparavant. La dernière fois que des calculs similaires ont été effectués remonte aux années 1960 par des scientifiques spatiaux soviétiques, en utilisant des données du côté de la lune visible depuis la Terre.

Cziráki, étudiante en géosciences de deuxième année spécialisée en géophysique, a travaillé avec son superviseur, Timár, pour calculer les paramètres de l'ellipsoïde rotatif qui s'adapte le mieux à la forme théorique de la lune.

Pour ce faire, ils ont utilisé une base de données d'une surface potentielle existante, appelée « lunar selenoid », à partir de laquelle ils ont pris un échantillon de hauteur à des points régulièrement espacés sur la surface et ont recherché les axes semi-majeur et semi-mineur qui s'adaptent le mieux à un ellipsoïde rotatif. En augmentant progressivement le nombre de points d'échantillonnage de 100 à 100 000, les valeurs des deux paramètres se sont stabilisées à 10 000 points.

L'une des principales étapes du travail a consisté à étudier comment disposer N points uniformément sur une surface sphérique, avec plusieurs solutions possibles ; Cziráki et Timár ont choisi la plus simple, appelée sphère de Fibonacci. La spirale de Fibonacci correspondante peut être implémentée avec un code très court et intuitif, et les fondements de cette méthode ont été posés par le mathématicien Leonardo Fibonacci il y a 800 ans. La méthode a également été appliquée à la Terre comme vérification, permettant de reconstruire une bonne approximation de l'ellipsoïde WGS84 utilisé par le GPS.

Fourni par l'Université Eötvös Loránd