Lo studio rivela l'esistenza della catastrofe del codone in sistemi non-Hermitiani.

19 giugno 2023 funzionalità

Questo articolo è stato revisionato secondo il processo editoriale e le politiche di Science X. Gli editori hanno evidenziato i seguenti attributi garantendo la credibilità del contenuto:

• verificato sui fatti
• pubblicazione sottoposta a revisione paritaria
• fonte affidabile
• verificato la correttezza

da Ingrid Fadelli, Phys.org

Ricercatori dell'Università di Scienza e Tecnologia di Hong Kong, dell'Università di Xiangtan e dell'Università di Scienza e Tecnologia del Sud hanno recentemente rivelato una possibile connessione tra la teoria delle catastrofi, un'area della matematica che si concentra sulla modellizzazione dei cambiamenti improvvisi (cioè le catastrofi) e la fisica non-hermitiana. Il loro articolo, pubblicato su Nature Physics, dimostra specificamente che una degenerazione strutturalmente ricca, conosciuta come catastrofe a coda d'aronde, può esistere naturalmente in sistemi non-hermitiani.

'Il nostro lavoro è stato ispirato da precedenti ricerche che hanno utilizzato la teoria dell'omotopia per classificare le singolarità topologiche, una tecnica che è stata utilizzata per studiare i difetti nei cristalli liquidi come le disclinenze e le dislocazioni,' ha detto Hongwei Jia, uno dei ricercatori che ha condotto lo studio, a Phys.org. 'La teoria dell'omotopia è stata applicata anche nella teoria delle bande per investigare la topologia delle bande non-abeliane. Sulla base di questi lavori precedenti, abbiamo cercato di estendere l'approccio per capire le singolarità (manifestate come degenerazioni chiamate punti eccezionali) in sistemi non-hermitiani.'

In sostanza, Jia, Chan ei loro colleghi hanno cercato di applicare il concetto di rotazione del telaio di autovettori lungo un loop che circonda una singolarità (cioè un punto in cui una funzione 'salta' o 'collassa') a sistemi non-hermitiani. Mentre in altri recenti studi su sistemi hermitiani, gli autovettori erano reali ed ortogonali, formando la base ortonormale di uno spazio euclideo, l'applicazione di questa rotazione del telaio di autovettori a sistemi non-hermitiani presenta una serie di sfide.

'In questi sistemi non-hermitiani, gli autovettori non sono ortogonali, poiché la relazione ortogonale degli autovettori è definita da un prodotto interno definito del tipo Minkowski. Quindi, lungo un percorso chiuso, il telaio di autovettori non solo ruota, ma si deforma anche. In particolare, quando il percorso incontra le superfici eccezionali, gli autovettori si fondono,' ha spiegato Jia.

'Questo pone un grave problema perché i loop omotopici convenzionali non tagliano mai attraverso le degenerazioni. Ma ciò non può essere evitato nel nostro caso, poiché le linee di degenerazione considerate sono interamente integrate su superfici eccezionali. Nell'affrontare queste difficoltà matematicamente impegnative, abbiamo cercato l'assistenza del matematico Yifei Zhu. Questa collaborazione tra fisici e matematici ha portato a nuovi insights sulle proprietà topologiche delle singolarità nei sistemi non-hermitiani.'

In collaborazione con Zhu, Jia, Chan ei loro colleghi hanno esplorato la comparsa di degenerazioni, denominate superfici eccezionali, singolarità isolate e non isolate, nei sistemi non-hermitiani, e la dipendenza di queste degenerazioni dalla simmetria. Per farlo, hanno seguito i punti di intersezione nella discriminante del polinomio caratteristico delle matrici di Hamilton sotto simmetrie specifiche nello spazio dei parametri.

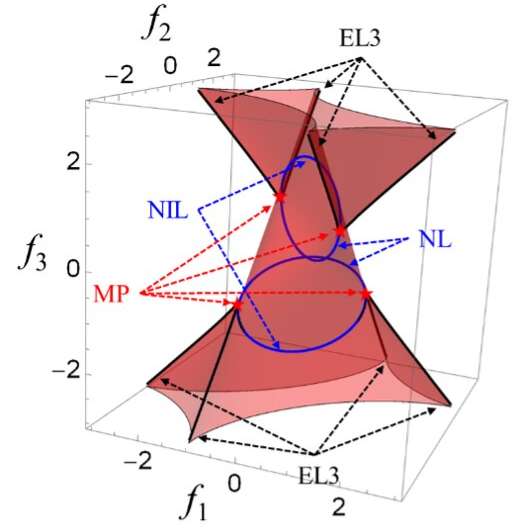
'Abbiamo condotto molti esperimenti matematici utilizzando vari strumenti, come software matematici, modelli in carta e stampa 3D,' ha detto Jia. 'Analizzando esempi espliciti di Hamiltoniani con simmetrie specifiche, abbiamo scoperto che la comparsa di questa singolarità è universale nei sistemi non-hermitiani con le nostre simmetrie scelte. Abbiamo anche dimostrato che possono esserci linee eccezionali di ordine tre (EL3) alle cuspidi delle superfici eccezionali, linee di intersezione non difettose (NIL) dove le superfici eccezionali si incontrano trasversalmente e linee di nodi (NL) isolate dalle superfici eccezionali.'

Gli esperimenti e i calcoli effettuati da Jia e dai suoi colleghi hanno portato a diversi interessanti risultati. Innanzitutto, il team ha scoperto che le diverse linee di degenerazione osservate possono sempre essere collegati stabilmente in un unico punto di incontro e che questa struttura unica è protetta dalla simmetria.

'Abbiamo osservato che le superfici eccezionali si intersecano in una configurazione a coda di rondine, che ricorda la catastrofe a coda di rondine in matematica e nella teoria delle catastrofi (in particolare nella classificazione ADE),' ha detto Jia. 'Tuttavia, ci sono notevoli differenze tra il nostro caso e la catastrofe a coda di rondine in classificazione ADE, poiché quest'ultima è descritta esaminando il luogo delle radici multiple di un polinomio quartico mentre la nostra sorge dalle simmetrie che stiamo studiando che codificano le evoluzioni degli autovettori.'

The recent work by this team of researchers establishes a connection between the mathematical catastrophe theory and non-Hermitian physics, two areas of study that were previously perceived as unrelated. Using homotopical methods, the team tried to gain a topological understanding of non-isolated singularities in non-Hermitian systems.

Jia and his colleagues ultimately unveiled several interesting new transitions that occur within the swallowtail structure of the catastrophe they observed. Notably, these counter-intuitive transition phenomena are protected in ways that previous research had not yet identified.

'This work is the result of a collaboration between myself and fellow physicist Che Ting Chan and mathematician Yifei Zhu,' Jia said. 'The introduction of intersection homotopy theory by Yifei is crucial in solving the problem. We combined our theory of eigen-frame deformation and rotation with intersection homotopy, and successfully demonstrated that the interesting transition phenomenon in a swallowtail is topologically protected. We believe there may be other interesting physical phenomena to be discovered in these platforms. Our complementary knowledge will enable us to further explore this uncharted area of research.'

The swallowtail catastrophe that Jia and his colleagues observed in non-Hermitian bands is an entirely new type of topological gapless phase. Further examinations of this phase could potentially unveil new physical phenomena and effects. The researchers are now conducting studies focusing on two intriguing phenomena, the first of which is the bulk–edge correspondence in this new type of gapless phase.

'We are exploring whether the gapless phases inherent in a swallowtail structure can also support topological edge states,' Jia said. 'The second phenomenon we are exploring is the unconventional bulk-Fermi arc that links the pair of exceptional lines of order three at paired cusps.'

In addition to informing future physics studies, the findings gathered by this team of researchers could lead to new research in the field of mathematics. Jia and his colleagues feel that the mathematical component of their work is still ad hoc and incomplete, and they plan to further develop it in their next works.

'In theory, despite the objects of study can already be formulated purely mathematically (in ADE classification), this formulation only gives the apparently comparable structure, while the underlying characteristics are quite different from the current case,' Jia explained. 'For example, the meeting point of the swallowtail in ADE classification is an exceptional point of order four, but that of the current swallowtail is a three-fold degeneracy affording two linearly independent eigenstates.

'It would be a real challenge and opportunity to get hold of mathematically systematic, physically meaningful, and experimentally realizable structures underneath this tip of an iceberg. We also believe that the algebraic method, intersection homotopy/homology, should be further developed, because it is a powerful tool for understanding such non-isolated singularities both in physics and mathematics.'

Journal information: Nature Physics

© 2023 Science X Network