Estudio revela la existencia de la catástrofe de la cola de golondrina en sistemas no-hermíticos.

19 de junio de 2023 feature

Este artículo ha sido revisado de acuerdo al proceso editorial y políticas de Science X. Los editores han destacado las siguientes características mientras aseguraban la credibilidad del contenido:

• verificación de hechos
• publicación evaluada por pares
• fuente confiable
• corrección de errores

por Ingrid Fadelli, Phys.org

Investigadores de la Universidad de Ciencia y Tecnología de Hong Kong, la Universidad de Xiangtan y la Universidad de Ciencia y Tecnología del Sur recientemente revelaron una posible conexión entre la teoría de las catástrofes, un área de las matemáticas que se centra en modelar cambios repentinos (es decir, catástrofes) y la física no Hermitiana. Su estudio, publicado en Nature Physics, muestra específicamente que una degeneración estructuralmente rica, conocida como la catástrofe de la cola de golondrina, puede existir naturalmente en sistemas no Hermitianos. googletag.cmd.push(function() { googletag.display('div-gpt-ad-1449240174198-2'); });

'Nuestro trabajo fue inspirado por investigación previa que utilizó la teoría de homotopía para clasificar las singularidades topológicas, una técnica que ha sido utilizada para estudiar defectos en cristales líquidos como las disclinas y dislocaciones', dijo Hongwei Jia, uno de los investigadores que llevó a cabo el estudio, a Phys.org. 'La teoría de homotopía también ha sido aplicada en la teoría de bandas para investigar la topología de banda no Abelian. Basándonos en estos trabajos previos, buscamos extender el enfoque para entender las singularidades (manifestadas como degeneraciones llamadas puntos excepcionales) en sistemas no Hermitianos.'

Esencialmente, Jia, Chan y sus colegas se propusieron aplicar el concepto de una rotación del marco de eigenvectores a lo largo de un bucle que rodea una singularidad (es decir, punto en el que una función "salta" o "colapsa") a sistemas no Hermitianos. Mientras que en otros estudios recientes sobre sistemas Hermitianos, los eigenvectores eran reales y ortogonales, formando la base ortogonal de un espacio Euclidiano, aplicar esta rotación de marco de eigenvectores a sistemas no Hermitianos plantea una serie de desafíos.

'En estos sistemas no Hermitianos, los eigenvectores no son ortogonales porque la relación ortogonal de eigenvectores está definida por un producto interno indefinido de tipo Minkowski. Por lo tanto, a lo largo de una trayectoria cerrada, el marco de eigenvectores no solo gira sino que también se deforma. Particularmente, cuando la trayectoria encuentra superficies excepcionales, los eigenvectores se fusionan', explicó Jia.

'Esto plantea un grave problema porque las ciclos homotópicos convencionales nunca cortan las degeneraciones. Pero esto no puede evitarse en nuestro caso, porque las líneas de degeneración consideradas están completamente incrustadas en superficies excepcionales. En la resolución de estas dificultades matemáticas, buscamos la ayuda del matemático Yifei Zhu. Esta colaboración entre físicos y matemáticos resultó en nuevos conocimientos sobre las propiedades topológicas de las singularidades en sistemas no Hermitianos.'

En colaboración con Zhu, Jia, Chan y sus colegas se propusieron explorar la aparición de degeneraciones, referidas como superficies excepcionales, singularidades aisladas y no aisladas, en sistemas no Hermitianos, y la dependencia de estas degeneraciones en la simetría. Para lograr esto, rastrearon los ceros en el discriminante del polinomio característico de las matrices Hamiltonianas bajo simetrías específicas en el espacio de parámetros.

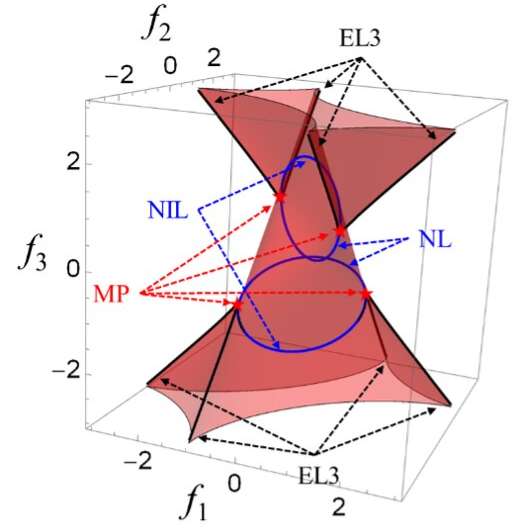
'Realizamos muchos experimentos matemáticos utilizando varias herramientas como software matemático, modelos en papel e impresión 3D', dijo Jia. 'Al analizar ejemplos explícitos de Hamiltonianos con simetrías específicas, descubrimos que la aparición de esta singularidad es universal en sistemas no Hermitianos con nuestras simetrías elegidas. También demostramos que pueden haber líneas excepcionales de orden tres (EL3) en las cúspides de las superficies excepcionales, líneas de intersección no defectuosas (NIL) donde las superficies excepcionales se intersectan transversalmente, y líneas nodales (NL) aisladas de las superficies excepcionales.'

Los experimentos y cálculos realizados por Jia y sus colegas revelaron varios hallazgos interesantes. En primer lugar, el equipo encontró que las distintas líneas de degeneración que observaron siempre pueden conectarse de manera estable en un solo punto de encuentro y que esta estructura única está protegida por simetría.

'Observamos que las superficies excepcionales se intersectan en una configuración en forma de cola de golondrina, lo que recuerda a la catástrofe de la cola de golondrina en matemáticas y la teoría de las catástrofes (específicamente en la clasificación de ADE)', dijo Jia. 'Sin embargo, hay diferencias notables entre nuestro caso y la catástrofe de la cola de golondrina en la clasificación de ADE, ya que esta última se describe examinando el lugar de las raíces múltiples de un polinomio cuártico mientras que la nuestra surge de las simetrías que estamos estudiando que codifican información de las evoluciones de los eigenvectores'.

The recent work by this team of researchers establishes a connection between the mathematical catastrophe theory and non-Hermitian physics, two areas of study that were previously perceived as unrelated. Using homotopical methods, the team tried to gain a topological understanding of non-isolated singularities in non-Hermitian systems.

Jia and his colleagues ultimately unveiled several interesting new transitions that occur within the swallowtail structure of the catastrophe they observed. Notably, these counter-intuitive transition phenomena are protected in ways that previous research had not yet identified.

'This work is the result of a collaboration between myself and fellow physicist Che Ting Chan and mathematician Yifei Zhu,' Jia said. 'The introduction of intersection homotopy theory by Yifei is crucial in solving the problem. We combined our theory of eigen-frame deformation and rotation with intersection homotopy, and successfully demonstrated that the interesting transition phenomenon in a swallowtail is topologically protected. We believe there may be other interesting physical phenomena to be discovered in these platforms. Our complementary knowledge will enable us to further explore this uncharted area of research.'

The swallowtail catastrophe that Jia and his colleagues observed in non-Hermitian bands is an entirely new type of topological gapless phase. Further examinations of this phase could potentially unveil new physical phenomena and effects. The researchers are now conducting studies focusing on two intriguing phenomena, the first of which is the bulk–edge correspondence in this new type of gapless phase.

'We are exploring whether the gapless phases inherent in a swallowtail structure can also support topological edge states,' Jia said. 'The second phenomenon we are exploring is the unconventional bulk-Fermi arc that links the pair of exceptional lines of order three at paired cusps.'

In addition to informing future physics studies, the findings gathered by this team of researchers could lead to new research in the field of mathematics. Jia and his colleagues feel that the mathematical component of their work is still ad hoc and incomplete, and they plan to further develop it in their next works.

'In theory, despite the objects of study can already be formulated purely mathematically (in ADE classification), this formulation only gives the apparently comparable structure, while the underlying characteristics are quite different from the current case,' Jia explained. 'For example, the meeting point of the swallowtail in ADE classification is an exceptional point of order four, but that of the current swallowtail is a three-fold degeneracy affording two linearly independent eigenstates.

'It would be a real challenge and opportunity to get hold of mathematically systematic, physically meaningful, and experimentally realizable structures underneath this tip of an iceberg. We also believe that the algebraic method, intersection homotopy/homology, should be further developed, because it is a powerful tool for understanding such non-isolated singularities both in physics and mathematics.'

Journal information: Nature Physics

© 2023 Science X Network