Studie enthüllt die Existenz der swallowtail-Katastrophe in nicht-hermiteschen Systemen.

The recent work by this team of researchers establishes a connection between the mathematical catastrophe theory and non-Hermitian physics, two areas of study that were previously perceived as unrelated. Using homotopical methods, the team tried to gain a topological understanding of non-isolated singularities in non-Hermitian systems.

Jia and his colleagues ultimately unveiled several interesting new transitions that occur within the swallowtail structure of the catastrophe they observed. Notably, these counter-intuitive transition phenomena are protected in ways that previous research had not yet identified.

'This work is the result of a collaboration between myself and fellow physicist Che Ting Chan and mathematician Yifei Zhu,' Jia said. 'The introduction of intersection homotopy theory by Yifei is crucial in solving the problem. We combined our theory of eigen-frame deformation and rotation with intersection homotopy, and successfully demonstrated that the interesting transition phenomenon in a swallowtail is topologically protected. We believe there may be other interesting physical phenomena to be discovered in these platforms. Our complementary knowledge will enable us to further explore this uncharted area of research.'

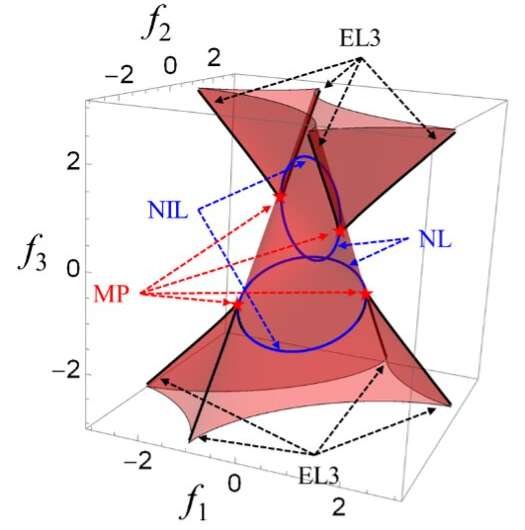
The swallowtail catastrophe that Jia and his colleagues observed in non-Hermitian bands is an entirely new type of topological gapless phase. Further examinations of this phase could potentially unveil new physical phenomena and effects. The researchers are now conducting studies focusing on two intriguing phenomena, the first of which is the bulk–edge correspondence in this new type of gapless phase.

'We are exploring whether the gapless phases inherent in a swallowtail structure can also support topological edge states,' Jia said. 'The second phenomenon we are exploring is the unconventional bulk-Fermi arc that links the pair of exceptional lines of order three at paired cusps.'

In addition to informing future physics studies, the findings gathered by this team of researchers could lead to new research in the field of mathematics. Jia and his colleagues feel that the mathematical component of their work is still ad hoc and incomplete, and they plan to further develop it in their next works.

'In theory, despite the objects of study can already be formulated purely mathematically (in ADE classification), this formulation only gives the apparently comparable structure, while the underlying characteristics are quite different from the current case,' Jia explained. 'For example, the meeting point of the swallowtail in ADE classification is an exceptional point of order four, but that of the current swallowtail is a three-fold degeneracy affording two linearly independent eigenstates.

'It would be a real challenge and opportunity to get hold of mathematically systematic, physically meaningful, and experimentally realizable structures underneath this tip of an iceberg. We also believe that the algebraic method, intersection homotopy/homology, should be further developed, because it is a powerful tool for understanding such non-isolated singularities both in physics and mathematics.'

Journal information: Nature Physics

© 2023 Science X Network