L'étude révèle l'existence de la catastrophe du papillon dans des systèmes non-hermitiens.

19 juin 2023 fonctionnalité

Cet article a été examiné selon le processus éditorial et les politiques de Science X. Les éditeurs ont mis en évidence les attributs suivants tout en garantissant la crédibilité du contenu :

• vérification des faits
• publication examinée par des pairs
• source de confiance
• relecture

par Ingrid Fadelli, Phys.org

Des chercheurs de l'Université de sciences et technologies de Hong Kong, de l'Université de Xiangtan et de l'Université de sciences et technologies du Sud ont récemment dévoilé une possible connexion entre la théorie des catastrophes, une branche des mathématiques qui se concentre sur la modélisation des changements soudains (catastrophes), et la physique non hermitienne. Leur article, publié dans Nature Physics, montre spécifiquement qu'une dégénérescence riche en structure, connue sous le nom de catastrophe en queue d'hirondelle, peut naturellement exister dans des systèmes non hermitiens. 

'Notre travail a été inspiré par des recherches antérieures qui ont utilisé la théorie de l'homotopie pour classer les singularités topologiques, une technique qui a été utilisée pour étudier les défauts dans les cristaux liquides tels que les disclinations et les dislocations', a déclaré Hongwei Jia, l'un des chercheurs qui a mené l'étude, à Phys.org. 'La théorie de l'homotopie a également été appliquée dans la théorie des bandes pour étudier la topologie des bandes non abélienne. En nous appuyant sur ces travaux antérieurs, nous avons cherché à étendre cette approche pour comprendre les singularités (manifestées sous la forme de dégénérescences appelées points exceptionnels) dans des systèmes non hermitiens.'

Essentiellement, Jia, Chan et leurs collègues ont cherché à appliquer le concept d'une rotation de cadre d'eigenvecteurs le long d'une boucle encerclant une singularité (c'est-à-dire un point où une fonction 'saut vif' ou 's'effondre') à des systèmes non hermitiens. Alors que dans d'autres études récentes sur les systèmes hermitiens, les vecteurs propres étaient réels et orthogonaux, formant la base orthonormale d'un espace euclidien, l'application de cette rotation de cadre d'eigenvecteurs aux systèmes non hermitiens pose une série de défis.

'Dans ces systèmes non hermitiens, les vecteurs propres ne sont pas orthogonaux, car la relation orthogonale des vecteurs propres est définie par un produit intérieur indéfini de type Minkowski. Ainsi, le cadre d'eigenvecteurs ne tourne pas seulement le long d'un chemin fermé, mais se déforme également. En particulier, lorsque le chemin rencontre des surfaces exceptionnelles, les vecteurs propres se fusionnent', a expliqué Jia.

'Cela pose un grave problème car les boucles homotopiques conventionnelles ne traversent jamais les dégénérescences. Mais cela ne peut être évité dans notre cas, car les lignes de dégénérescence considérées sont entièrement intégrées sur des surfaces exceptionnelles. Pour résoudre ces difficultés mathématiques, nous avons demandé l'aide du mathématicien Yifei Zhu. Cette collaboration entre physiciens et mathématiciens a donné de nouvelles perspectives sur les propriétés topologiques des singularités dans les systèmes non hermitiens.'

En collaboration avec Zhu, Jia, Chan et leurs collègues ont exploré l'occurrence de dégénérescences, appelées surfaces exceptionnelles, singularités isolées et non isolées, dans des systèmes non hermitiens, ainsi que la dépendance de ces dégénérescences à la symétrie. Pour ce faire, ils ont suivi les zéros dans le discriminant du polynôme caractéristique des matrices hamiltoniennes sous des symétries spécifiques dans l'espace des paramètres.

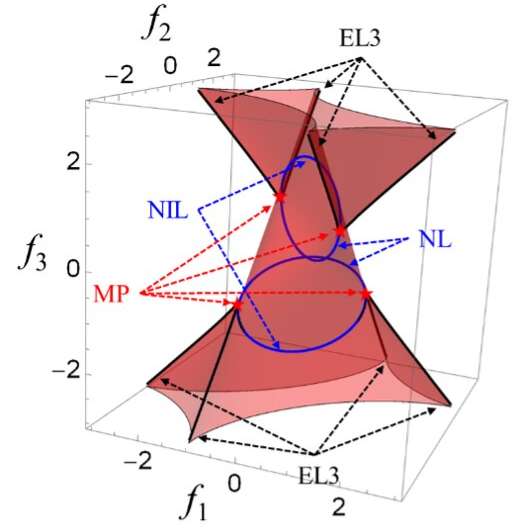
'Nous avons mené de nombreuses expériences mathématiques avec divers outils tels que des logiciels mathématiques, des modèles en papier et l'impression 3D', a déclaré Jia. 'En analysant des exemples explicites de hamiltoniens avec des symétries spécifiques, nous avons découvert que l'occurrence de cette singularité est universelle dans les systèmes non hermitiens avec les symétries choisies. Nous avons également démontré qu'il peut y avoir des lignes exceptionnelles d'ordre trois (EL3) au niveau des points de rebroussement des surfaces exceptionnelles, des lignes d'intersection non défectueuses (NIL) où les surfaces exceptionnelles se coupent de manière transversale, et des lignes nodales (NL) isolées des surfaces exceptionnelles.'

Les expériences et calculs réalisés par Jia et ses collègues ont abouti à plusieurs résultats intéressants. Tout d'abord, l'équipe a constaté que les lignes de dégénérescence distinctes qu'elle a observées peuvent toujours être connectées de manière stable en un seul point de rencontre, et que cette structure unique est protégée par la symétrie.

'Nous avons constaté que les surfaces exceptionnelles se croisent dans une configuration en queue d'hirondelle, qui rappelle la catastrophe en queue d'hirondelle en mathématiques et en théorie des catastrophes (en particulier en classification ADE)', a déclaré Jia. 'Cependant, il existe des différences notables entre notre cas et la catastrophe en queue d'hirondelle en classification ADE, car cette dernière est décrite en examinant le lieu des racines multiples d'un polynôme quartique, tandis que la nôtre découle des symétries que nous étudions qui codent les évolutions des eigenvecteurs.'

The recent work by this team of researchers establishes a connection between the mathematical catastrophe theory and non-Hermitian physics, two areas of study that were previously perceived as unrelated. Using homotopical methods, the team tried to gain a topological understanding of non-isolated singularities in non-Hermitian systems.

Jia and his colleagues ultimately unveiled several interesting new transitions that occur within the swallowtail structure of the catastrophe they observed. Notably, these counter-intuitive transition phenomena are protected in ways that previous research had not yet identified.

'This work is the result of a collaboration between myself and fellow physicist Che Ting Chan and mathematician Yifei Zhu,' Jia said. 'The introduction of intersection homotopy theory by Yifei is crucial in solving the problem. We combined our theory of eigen-frame deformation and rotation with intersection homotopy, and successfully demonstrated that the interesting transition phenomenon in a swallowtail is topologically protected. We believe there may be other interesting physical phenomena to be discovered in these platforms. Our complementary knowledge will enable us to further explore this uncharted area of research.'

The swallowtail catastrophe that Jia and his colleagues observed in non-Hermitian bands is an entirely new type of topological gapless phase. Further examinations of this phase could potentially unveil new physical phenomena and effects. The researchers are now conducting studies focusing on two intriguing phenomena, the first of which is the bulk–edge correspondence in this new type of gapless phase.

'We are exploring whether the gapless phases inherent in a swallowtail structure can also support topological edge states,' Jia said. 'The second phenomenon we are exploring is the unconventional bulk-Fermi arc that links the pair of exceptional lines of order three at paired cusps.'

In addition to informing future physics studies, the findings gathered by this team of researchers could lead to new research in the field of mathematics. Jia and his colleagues feel that the mathematical component of their work is still ad hoc and incomplete, and they plan to further develop it in their next works.

'In theory, despite the objects of study can already be formulated purely mathematically (in ADE classification), this formulation only gives the apparently comparable structure, while the underlying characteristics are quite different from the current case,' Jia explained. 'For example, the meeting point of the swallowtail in ADE classification is an exceptional point of order four, but that of the current swallowtail is a three-fold degeneracy affording two linearly independent eigenstates.

'It would be a real challenge and opportunity to get hold of mathematically systematic, physically meaningful, and experimentally realizable structures underneath this tip of an iceberg. We also believe that the algebraic method, intersection homotopy/homology, should be further developed, because it is a powerful tool for understanding such non-isolated singularities both in physics and mathematics.'

Journal information: Nature Physics

© 2023 Science X Network