Utiliser des excitations atomiques pour mesurer la rotation de l'espace-temps

Le 29 août 2024 Cette article a été examinée selon les processus éditoriaux et les politiques de Science X. 

Les rédacteurs ont mis en évidence les attributs suivants tout en garantissant la crédibilité du contenu: 

• vérification des faits, 
• prépublication,
•  source fiable,
•  relecture par 

David Appell de Phys.org.

 Comment les atomes se comporteraient-ils près d'un objet supermassif? 

Nous savons comment les atomes se comportent dans une gravité extrêmement faible comme celle à la surface de la Terre: ils peuvent être excités d'un niveau énergétique inférieur à un niveau supérieur lorsqu'un électron absorbé un photon ou un noyau absorbé un rayon gamma, et ainsi de suite. Mais que se passe-t-il si l'atome est dans un champ gravitationnel fort comme celui près d'un trou noir supermassif en rotation ou d'une étoile à neutrons en rotation? Deux scientifiques du Beijing Computational Science Research Center en Chine ont déterminé que le niveau d'excitation dépendrait également de la vitesse à laquelle l'espace-temps tourne à l'extérieur de l'objet massif. 

En fait, ils affirment que l'image inverse pourrait être utile: mesurer les changements dans un ensemble d'excitations pourrait servir à déterminer à quelle vitesse l'espace-temps tourne, un phénomène appelé entraînement de l'inertie. Les résultats sont publiés sur le serveur de prépublication arXiv. L'entraînement de l'inertie est une prédiction de la théorie de la gravitation d'Einstein appelée relativité générale. 

Tout comme un trou noir stationnaire déforme l'espace-temps autour de lui, créant un horizon des événements et une singularité apparente à son centre, en 1918, les physiciens autrichiens Josef Lense et Hans Thirring ont découvert que la rotation d'un objet massif entraînerait l'espace-temps à proximité dans la direction de rotation. Les mesures des distances et des angles seraient donc modifiées à proximité de la masse, et l'espace et le temps pourraient même être en partie mélangés par rapport à un observateur éloigné. 

Connue sous le nom d'effet Lense-Thirring, l'effet existe même dans la limite du 'champ faible' des équations d'Einstein, tout comme l'espace-temps près de l'horizon des événements d'un trou noir, où la gravité n'est pas excessivement forte (mais plus forte que sur Terre). La NASA et d'autres groupes ont trouvé des preuves astronomiques de l'entraînement de l'inertie, bien que les chercheurs estiment que les mesures doivent être affinées. 

La vélocité de rotation de l'entraînement de l'inertie dépend du moment angulaire de la masse (sa vitesse de rotation) et de la masse, ainsi que de la distance par rapport à celle-ci. Dans cette étude, les scientifiques ont supposé une petite masse (comme un atome ou un autre objet avec des niveaux d'énergie) entourée d'un champ quantique simple qui existe partout à l'extérieur de la masse centrale en rotation. Les particules associées au champ quantique ont un spin nul (au sens quantique); un exemple en serait un champ électromagnétique, où les vecteurs de force du champ, les photons, ont un spin nul. 

La fréquence angulaire de l'entraînement de l'inertie serait-elle reflétée dans le taux d'excitation d'un atome? Dans le cas plus simple d'un trou noir non rotatif, la soi-disant 'solution de Schwarzschild' aux équations d'Einstein, il n'y a pas d'entraînement de l'inertie. Il est connu qu'un atome au repos serait excité par le rayonnement de Hawking du trou noir, un rayonnement émis avec le spectre de fréquence d'un corps noir qui est émis à l'horizon des événements entourant le trou noir. Le taux d'excitation de l'atome contient des informations sur la force du champ gravitationnel à l'horizon des événements. 

Cependant, pour un trou noir massif en rotation, qui a la soi-disant 'solution de Kerr' (qui n'a été trouvée qu'en 1963), il n'y a pas de véritables horizons des événements et singularités. L'espace-temps de Kerr présente un entraînement de l'inertie, mais un atome au repos ne serait pas excité. Contrairement à la solution de Schwarzschild, la solution de Kerr est une solution exacte pour la structure de l'espace-temps même pour des masses très grandes et une forte gravité. Ainsi, les co-auteurs Rui-Chen Liu et C. P. Sun ont pris en compte le cas d'un atome se déplaçant en cercle à vitesse constante dans l'espace-temps de Kerr. Ils ont 'quantifié' le champ de spin nul, c'est-à-dire qu'ils l'ont traité conformément aux règles de la mécanique quantique (qui est différente des célèbres équations de Maxwell qui traitent les champs électromagnétiques comme classiques, sans photons ou particules à spin nul.)

 En mettant tout cela ensemble et en travaillant à travers les mathématiques, les deux ont découvert qu'un atome serait excité. Ils ont en outre constaté que le taux d'excitation - le nombre d'excitations par seconde - est le même que celui d'un atome immergé dans un bain thermique (entouré d'énergie) à une température proportionnelle à l'accélération de l'atome lorsqu'il tourne en cercle. Cela ressemble à l'effet Unruh, dans lequel un atome subissant une accélération constante dans le vide, même en ligne droite, verrait des particules et un bain thermique avec une température extrêmement faible mais non nulle.

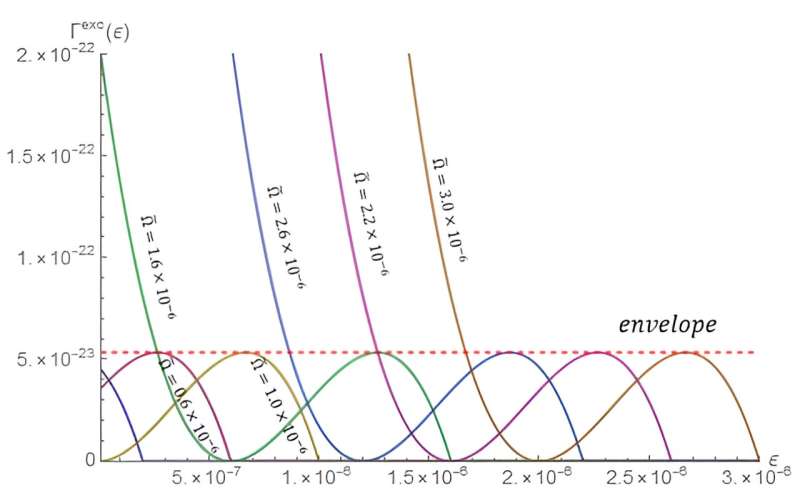
Pour approfondir leur analyse, Liu et Sun ont examiné diverses énergies d'excitation pour les atomes tournant à des vitesses différentes et à différentes distances de la masse centrale et ont constaté que les taux d'excitation se situaient tous entre 0 et une limite supérieure pour toutes les valeurs de la fréquence de rotation de traînée du cadre.

Ils écrivent, "L'effet de traînée du cadre génère un taux d'excitation distinct pour les atomes effectuant un mouvement circulaire." Cette limite supérieure pourrait être mesurée, et la vitesse de rotation de la fréquence de rotation de traînée du cadre pourrait en être déduite et le rayon du mouvement.

Ils notent que leur approche utilise les propriétés non locales des champs quantiques, également connues sous le nom d'entanglement, en utilisant des mesures qui ne dépendent pas de l'étalonnage stellaire traditionnel, qui utilise des étoiles aux propriétés lumineuses connues pour déterminer la qualité et la fiabilité des capteurs sur un télescope.

Plus d'informations: Rui-Chen Liu et al, L'effet de traînée du cadre sur le taux d'excitation des atomes, arXiv (2024). DOI: 10.48550/arxiv.2408.13016

Informations sur la revue: arXiv

© 2024 Réseau Science X