Användning av atomära excitationer för att mäta rotationen av rumtid

Den 29 augusti 2024 i funktion Detta artikel har granskats enligt Science X's redaktionella process och policys. 

Redaktörerna har framhävt följande egenskaper samtidigt som de säkerställde innehållets trovärdighet: 

• kontrollerad fakta 
• publicerade för tryckning pålitlig 
• källa korrekturläst 

av David Appell, 

Phys.orgHur skulle atomer bete sig nära ett supermassivt objekt? Vi vet hur atomer beter sig vid extremt svag gravitation som på jordens yta: De kan exciteras från en lägre energinivå till en högre när en elektron absorberar en foton eller en kärna absorberar en gammastråle, och så vidare. Men vad händer om atomen befinner sig i ett starkt gravitationsfält som ett nära en supermassiv, roterande svart hål eller roterande neutronstjärna?Två forskare från Beijing Computational Science Research Center i Kina har kommit fram till att mängden excitation också skulle bero på hur snabbt rymdtiden snurrar runt utanför det massiva objektet. Faktum är att de säger att den omvända bilden kan vara användbar: Att mäta förändringarna i en uppsättning excitationer kan användas för att bestämma hur snabbt rymdtiden snurrar, ett fenomen som kallas ramdragning.Fynden är publicerade på arXiv preprint server.

Ramdragning är en förutsägelse av Einsteins teori om gravitation kallad allmänna relativitetsteorin. Precis som en stationär svart hål deformerar rymdtiden runt omkring det, vilket resulterar i en händelsehorisont och en uppenbar singularitet i mitten, fann österrikiska fysiker Josef Lense och Hans Thirring 1918 att rotationen av ett massivt objekt skulle dra rymdtiden nära det i riktning mot rotationen.

Avstånd och vinkeluttag skulle därför förändras nära massan, och rum och tid kan till och med vara delvis blandade relativa en iakttagare långt bort.Känt som Lense-Thirring-effekten, finns effekten även i 'svagt fält' gränsen av Einsteins ekvationer, samma som rymdtiden nära ett svart håls händelsehorisont, där tyngdkraften inte är alltför stark (men starkare än på jorden).NASA och andra grupper har hittat astronomiska bevis på ramdragning, även om forskarna säger att mätningarna behöver förtydligas. 

Den roterande hastigheten för dragning beror på massans vinkelmomentum (hur snabbt den roterar) och massa, samt avståndet bort från den. I denna studie antog forskarna en liten massa (som en atom eller annat objekt med energinivåer) omgiven av ett enkelt kvantfält som finns överallt utanför den centrala roterande massan.Halvornas associerade partiklar har nollspinn (i den kvantmekaniska meningen); ett exempel skulle vara ett elektromagnetiskt fält, där fältets kraftbärare, fotoner, har nollspinn. Skulle ramdragningens vinkelhastighet återspeglas i exciteringsfrekvensen för en atom?

I det enklare fallet med ett icke-roterande svart hål, den så kallade "Schwarzschild-lösningen" till Einsteins ekvationer, finns ingen ramdragning. Det är känt att en atom i vila skulle exciteras av svart håls Hawking-strålning, strålning som utsänds med frekvensspektrumet för en svart kropp som släpps ut vid händelsehorisonten som omger det svarta hålet. Exciteringsfrekvensen för atomen innehåller information om styrkan hos det gravitationella fältet vid händelsehorisonten.

Men för ett roterande massivt svart hål, som har den så kallade "Kerr-lösningen" (som inte hittades förrän 1963), finns det inga verkliga händelsehorisonter och singulariteter. Kerr-tidsrummet uppvisar visserligen ramdragning, men en atom i vila skulle inte exciteras.

Till skillnad från Schwarzschild-lösningen är Kerr-lösningen en exakt lösning för strukturen i rymdtiden även för mycket stora massor och stark gravitation. Så medförfattarna Rui-Chen Liu och C. P. Sun övervägde fallet med en atom som rör sig i en cirkel med konstant hastighet i Kerr-tidsrummet.

De 'kvantifierade' nollspinnfältet, det vill säga hanterade det enligt reglerna för kvantmekanik (som skiljer sig från de berömda Maxwells ekvationer som behandlar de elektromagnetiska fälten som klassiska, utan fotoner eller nollspinnpartiklar.) Genom att sätta allt detta ihop och arbeta igenom matematiken fann de två att en atom skulle komma att exciteras.

De fann vidare att exciteringsfrekvensen - antalet excitationer per sekund - är samma som för en atom som omges av ett termiskt bad (omgiven av energi) vid en temperatur som är proportionell mot atomens acceleration när den går runt i en cirkel. 

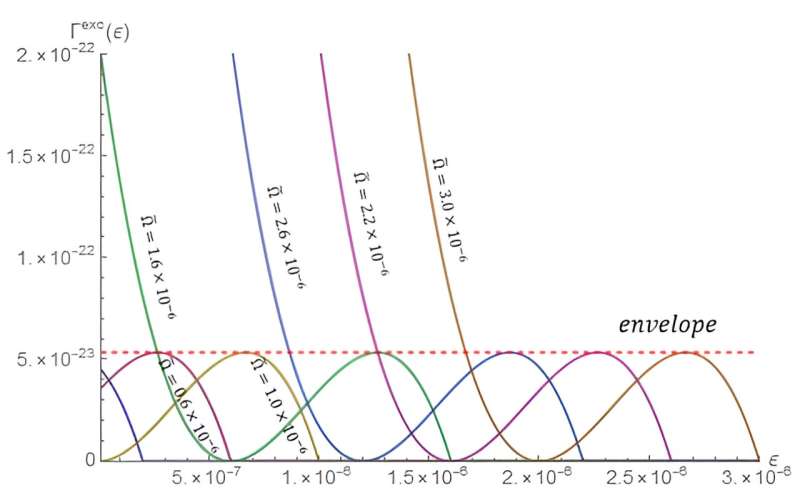
Detta liknar Unruh-effekten, där en atom som undergår en konstant acceleration i ett tomt vakuum, även i en rak linje, skulle se partiklar och ett termiskt bad med en extremt liten men icke-noll temperatur.För att fördjupa sin analys, tog Liu och Sun i beaktande olika exciteringsenergier för atomer som roterar i olika hastigheter och avstånd från massans mittpunkt och fann att exciteringshastigheterna alla låg mellan 0 och en övre gräns för alla värden på ramdragningens rotationsfrekvens. De skriver, 'Ramdragningseffekten genererar en distinkt exciteringshastighet för atomer som genomgår cirkulär rörelse.' 

Denna övre gräns kan mätas, och rotationshastigheten hos ramdragningens rotationsfrekvens kan härledas från den och rörelsens radie. De noterar att deras tillvägagångssätt använder icke-lokala egenskaper hos kvantfält, även känd som förflätning, genom att använda mätningar som inte är beroende av traditionell stjärnkalibrering, vilket använder stjärnor med kända ljusegenskaper för att fastställa kvaliteten och tillförlitligheten hos sensorer på ett teleskop. Mer information: Rui-Chen Liu et al, Frame-Dragging-effekten på exciteringshastigheten hos atomer, arXiv (2024). DOI: 10.48550/arxiv.2408.13016 Tidskriftsinformation: arXiv © 2024 Science X Network