Measuring Spacetime Rotation Through Atomic Excitations

August 29, 2024 feature

This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:

• fact-checked
• preprint
• trusted source
• proofread

by David Appell , Phys.org

How would atoms behave near a supermassive object? We know how atoms behave in extremely weak gravity like that at the Earth's surface: They can be excited from a lower energy level to a higher one when an electron absorbs a photon or a nucleus absorbs a gamma ray, and so on. But what if the atom is in a strong gravitational field such as one near a supermassive, rotating black hole or rotating neutron star?

Two scientists from Beijing Computational Science Research Center in China have determined that the amount of excitation would also depend on how fast spacetime is being spun around outside the massive object. In fact, they say, the reverse picture could be useful: Measuring the changes in a set of excitations might be used to determine how fast spacetime is rotating, a phenomenon called frame dragging.

The findings are posted on the arXiv preprint server.

Frame dragging is a prediction of Einstein's theory of gravity called general relativity. Just as a stationary black hole deforms spacetime around it, resulting in an event horizon and an apparent singularity at its center, in 1918 Austrian physicists Josef Lense and Hans Thirring found that the rotation of a massive object would drag spacetime near it around in the direction of rotation.

The measurements of distances and angles would thus be changed near the mass, and space and time might even be partly mixed up relative to an observer far away.

Known as the Lense–Thirring effect, the effect exists even in the 'weak field' limit of Einstein's equations, same as spacetime near a black hole's event horizon, where gravity isn't overly strong (but stronger than on Earth).

NASA and other groups have found astronomical evidence of frame dragging, though researchers say the measurements need to be tightened up. The rotational velocity of dragging depends on the mass's angular momentum (how fast it is rotating) and mass, as well as the distance away from it.

In this study, the scientists assumed a small mass (such as an atom or other object with energy levels) surrounded by a simple quantum field that exists everywhere outside the central rotating mass.

The quantum field's associated particles have zero spin (in the quantum mechanical sense); one example would be an electromagnetic field, where the field's force carriers, photons, have zero spin. Would the angular frequency of frame dragging be reflected in the excitation rate of an atom?

In the simpler case of a nonrotating black hole, the so-called 'Schwarzschild solution' to Einstein's equations, there is no frame dragging. It's known that an atom at rest would be excited by the black hole's Hawking radiation, radiation emitted with the frequency spectrum of a blackbody that is released at the event horizon surrounding the black hole. The excitation rate of the atom contains information about the strength of the gravitational field at the event horizon.

However, for a rotating massive black hole, which has the so-called 'Kerr solution' (which wasn't found until 1963), there are no true event horizons and singularities. The Kerr spacetime does exhibit frame dragging, but an atom at rest would not be excited.

Unlike the Schwarzschild solution, the Kerr solution is an exact solution for the structure of spacetime even for very large masses and strong gravity. So co-authors Rui-Chen Liu and C. P. Sun considered the case of an atom traveling in a circle at constant speed in Kerr spacetime.

They 'quantized' the zero-spin field, that is, treated it in accord with the rules of quantum mechanics (which are unlike the famous Maxwell equations that treat the electromagnetic fields as classical, with no photons or zero spin particles.) Putting all this together and working through the mathematics, the two found that an atom will be excited.

They further found that excitation rate—the number of excitations per second—is the same as that of an atom immersed in a thermal bath (surrounded by energy) at a temperature proportional to the atom's acceleration as it goes around in a circle. This is akin to the Unruh effect, in which an atom undergoing a constant acceleration in an empty vacuum, even in a straight line, would see particles and a thermal bath with an extremely small but nonzero temperature.

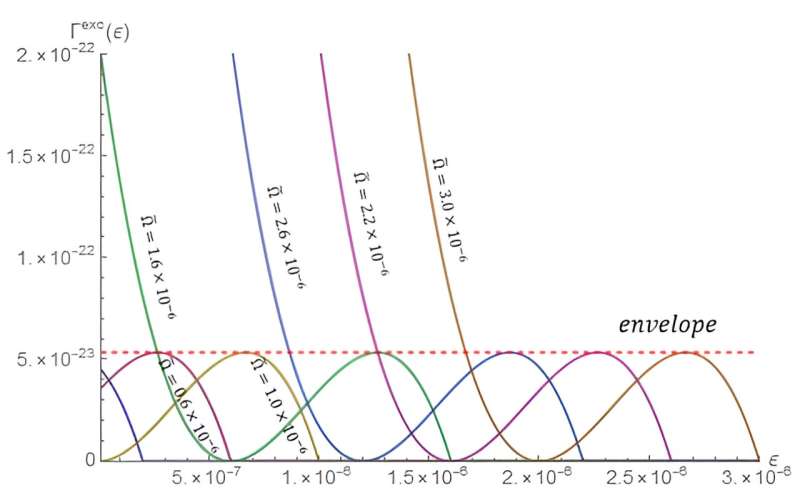
To further their analysis, Liu and Sun considered various excitation energies for atoms rotating at different speeds and different distances from the central mass and found that the excitation rates all appeared between 0 and an upper bound for all values of the frame dragging rotational frequency.

They write, 'The frame dragging effect generates a distinct excitation rate for atoms undergoing circular motion.' This upper bound could be measured, and the rotation rate of the frame dragging rotational frequency could be inferred from it and the motion's radius.

They note that their approach uses the non-local properties of quantum fields, also known as entanglement, using measurements that do not depend on traditional stellar calibration, which uses stars with known light properties to determine the quality and reliability of sensors on a telescope.

More information: Rui-Chen Liu et al, The Frame-Dragging effect on the excitation rate of atoms, arXiv (2024). DOI: 10.48550/arxiv.2408.13016

Journal information: arXiv

© 2024 Science X Network