Verwendung von atomaren Erregungen zur Messung der Rotation von Raum und Zeit

29. August 2024 feature

Dieser Artikel wurde gemäß dem Editorialprozess und den Richtlinien von Science X überprüft. Die Herausgeber haben die folgenden Attribute hervorgehoben, um die Glaubwürdigkeit des Inhalts zu gewährleisten:

• Faktencheck
• Preprint
• Vertrauenswürdige Quelle
• Korrekturgelesen

von David Appell, Phys.org

Wie würden sich Atome in der Nähe eines supermassiven Objekts verhalten? Wir wissen, wie sich Atome in extrem schwacher Schwerkraft verhalten, wie beispielsweise an der Oberfläche der Erde: Sie können von einem niedrigeren Energiestand zu einem höheren angeregt werden, wenn ein Elektron ein Photon absorbiert oder ein Atomkern ein Gammastrahlung absorbiert, und so weiter. Aber was ist, wenn das Atom in einem starken Gravitationsfeld ist, wie zum Beispiel in der Nähe eines supermassiven, rotierenden Schwarzen Lochs oder eines rotierenden Neutronensterns?

Zwei Wissenschaftler des Beijing Computational Science Research Center in China haben festgestellt, dass die Menge an Anregung auch davon abhängen würde, wie schnell der Raum außerhalb des massiven Objekts gedreht wird. Tatsächlich behaupten sie, dass das umgekehrte Bild nützlich sein könnte: Das Messen der Veränderungen in einer Gruppe von Anregungen könnte verwendet werden, um festzustellen, wie schnell der Raum gedreht wird, ein Phänomen, das als "frame dragging" bezeichnet wird.

Die Ergebnisse sind auf dem arXiv-Preprint-Server veröffentlicht.

Frame dragging ist eine Vorhersage von Einsteins Gravitationstheorie, die als Allgemeine Relativitätstheorie bekannt ist. Genau wie ein stationäres Schwarzes Loch den Raum um sich herum verformt, was zu einem Ereignishorizont und einer scheinbaren Singularität in seinem Zentrum führt, fanden die österreichischen Physiker Josef Lense und Hans Thirring 1918 heraus, dass die Rotation eines massiven Objekts den Raum in seiner Nähe in Rotationsrichtung mitziehen würde.

Die Messungen von Entfernungen und Winkeln würden daher in der Nähe der Masse verändert, und Raum und Zeit könnten im Vergleich zu einem weit entfernten Beobachter sogar teilweise vermischt sein.

Bekannt als der Lense-Thirring-Effekt, existiert dieser Effekt sogar im "schwachen Feld"-Limit von Einsteins Gleichungen, genauso wie der Raum außerhalb eines Ereignishorizonts eines Schwarzen Lochs, wo die Schwerkraft nicht übermäßig stark ist (aber stärker als auf der Erde).

Diverse Organisationen, einschließlich der NASA, haben astronomische Beweise für frame dragging gefunden, obwohl die Forscher sagen, dass die Messungen genauer gemacht werden müssen. Die Rotationsgeschwindigkeit des Drags hängt vom Drehimpuls der Masse (wie schnell sie sich dreht) und der Masse sowie der Entfernung von ihr ab.

In dieser Studie nahmen die Wissenschaftler an, dass eine geringe Masse (wie zum Beispiel ein Atom oder ein anderes Objekt mit Energieniveaus) von einem einfachen Quantenfeld umgeben ist, das überall außerhalb der zentralen Rotationsmasse existiert.

Die mit dem Quantenfeld verbundenen Teilchen haben keinen Spin (im quantenmechanischen Sinne); ein Beispiel wäre ein elektromagnetisches Feld, in dem die Feldträger, Photonen, keinen Spin haben. Würde die Winkelfrequenz des frame dragging in der Erregungsrate eines Atoms reflektiert werden?

In dem einfacheren Fall eines nicht rotierenden schwarzen Lochs, der sogenannten 'Schwarzschild-Lösung' von Einsteins Gleichungen, gibt es kein frame dragging. Es ist bekannt, dass ein ruhendes Atom durch die Hawking-Strahlung des Schwarzen Lochs erregt würde, einer Strahlung, die mit dem Frequenzspektrum eines Schwarzkörpers emittiert wird und am Ereignishorizont um das Schwarze Loch herum freigesetzt wird. Die Erregungsrate des Atoms enthält Informationen über die Stärke des Gravitationsfeldes am Ereignishorizont.

Allerdings, für ein rotierendes massives Schwarzes Loch, das die sogenannte 'Kerr-Lösung' hat (die erst 1963 gefunden wurde), gibt es keine echten Ereignishorizonte und Singularitäten. Der Kerr-Raum zeigt frame dragging, aber ein ruhendes Atom würde nicht erregt werden.

Anders als die Schwarzschild-Lösung ist die Kerr-Lösung eine genaue Lösung für die Struktur des Raums selbst für sehr große Massen und starke Gravitation. Daher betrachteten die Mitautoren Rui-Chen Liu und C. P. Sun den Fall eines Atoms, das mit konstanter Geschwindigkeit in Kreisen im Kerr-Raum bewegt.

Sie 'quantisierten' das Null-Spin-Feld, behandelten es also entsprechend den Regeln der Quantenmechanik (im Gegensatz zu den berühmten Maxwell-Gleichungen, die die elektromagnetischen Felder klassisch behandeln, ohne Photonen oder Teilchen mit keinem Spin.) Durch die Zusammenführung all dieser Informationen und das Durchrechnen der Mathematik fanden die beiden heraus, dass ein Atom erregt werden würde.

Weiter fanden sie heraus, dass die Erregungsrate - die Anzahl der Erregungen pro Sekunde - der gleichen entspricht wie die eines Atoms, das in einem thermischen Bad (umgeben von Energie) bei einer Temperatur, die proportional zur Beschleunigung des Atoms ist, das sich in einem Kreis bewegt. Dies ähnelt dem Unruh-Effekt, bei dem ein Atom, das einem konstanten Beschleunigung ausgesetzt ist, auch in einem leeren Vakuum, sogar in einer geraden Linie, Teilchen und ein thermisches Bad mit einer extrem geringen, aber nicht-nullen Temperatur sehen würde.

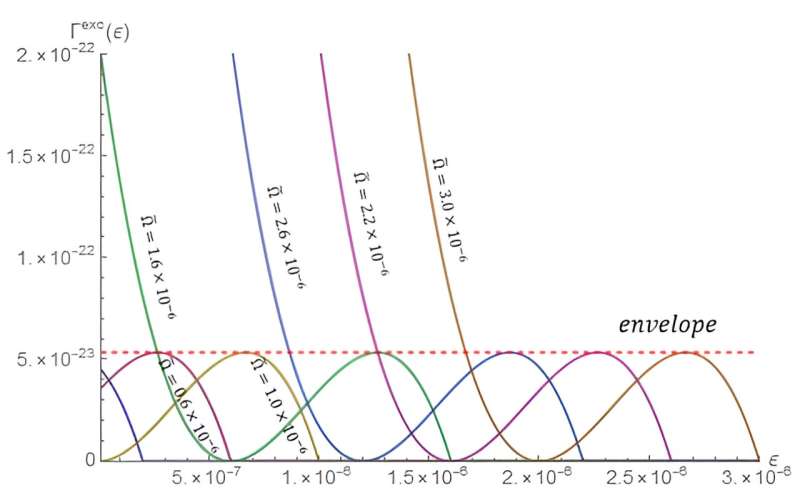
Um ihre Analyse weiter voranzutreiben, betrachteten Liu und Sun verschiedene Anregungsenergien für Atome, die sich mit unterschiedlichen Geschwindigkeiten drehen und sich in unterschiedlichen Abständen vom zentralen Massenpunkt befinden. Sie stellten fest, dass die Anregungsraten alle zwischen 0 und einem oberen Grenzwert für alle Werte der Rotationsfrequenz des Frame-Dragging lagen.

Sie schreiben: "Der Frame-Dragging-Effekt erzeugt eine deutliche Anregungsrate für Atome, die eine kreisförmige Bewegung durchlaufen." Dieser obere Grenzwert könnte gemessen werden, und die Rotationsrate der Rotationsfrequenz des Frame-Dragging könnte daraus abgeleitet werden und aus dem Radius der Bewegung.

Sie beachten, dass ihr Ansatz die nicht-lokalen Eigenschaften der Quantenfelder, auch als Verschränkung bekannt, nutzt, indem Messungen durchgeführt werden, die nicht von der traditionellen Kalibrierung der Sterne abhängen, bei der Sterne mit bekannten Lichteigenschaften verwendet werden, um die Qualität und Zuverlässigkeit von Sensoren an einem Teleskop zu bestimmen.

Weitere Informationen: Rui-Chen Liu et al, Der Frame-Dragging-Effekt auf die Anregungsrate von Atomen, arXiv (2024). DOI: 10.48550/arxiv.2408.13016

Journal Informationen: arXiv

© 2024 Science X Network