Hobbyista del Reino Unido deja perplejo al mundo de las matemáticas con nuevas formas "sorprendentes".

10 de junio de 2023

Este artículo ha sido revisado de acuerdo al proceso editorial y políticas de Science X. Los editores han destacado los siguientes atributos mientras aseguran la credibilidad del contenido:

• verificación de hechos
• agencia de noticias reputada
• corrección de pruebas

por Daniel Lawler

David Smith, un técnico retirado de impresión del norte de Inglaterra, estaba persiguiendo su hobby de buscar formas interesantes cuando tropezó con una diferente a cualquier otra en noviembre. 

Cuando Smith compartió su forma con el mundo en marzo, los fanáticos emocionados la imprimieron en camisetas, la cosieron en mantas, la utilizaron para hacer cortadores de galletas o para reemplazar los hexágonos de una pelota de fútbol, incluso algunos hicieron planes para tatuajes.

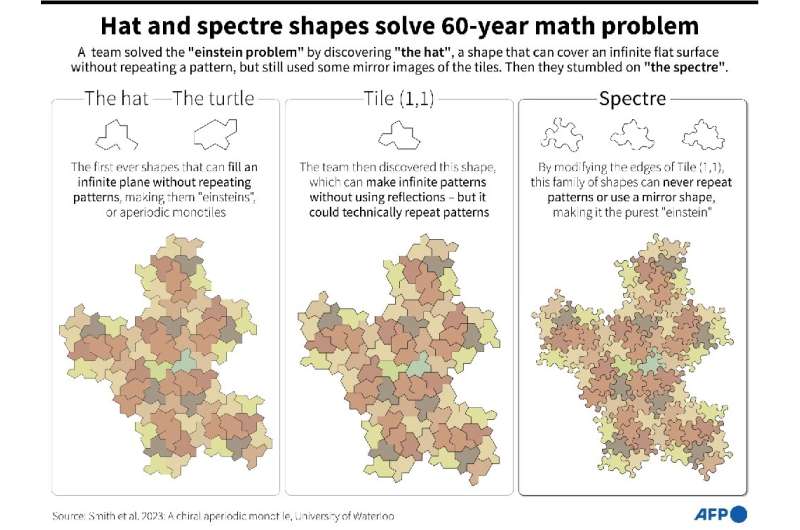
El polígono de 13 lados, al que Smith de 64 años llamó "el sombrero", es la primera forma única encontrada que puede cubrir por completo una superficie plana infinitamente grande sin repetir el mismo patrón.

Esto lo convierte en el primer "einstein", nombre dado en alemán por "una piedra" (ein stein), no por el famoso físico, y resuelve un problema planteado hace 60 años que algunos matemáticos pensaban que era imposible.

Después de sorprender al mundo de las matemáticas, Smith, un aficionado sin formación que le dijo a AFP que no era bueno en matemáticas en la escuela, lo hizo de nuevo.

Aunque todos estuvieron de acuerdo en que "el sombrero" era el primer einstein, su imagen en espejo era necesaria una de cada siete veces para garantizar que un patrón nunca se repitiera.

Pero en un estudio preimpreso publicado en línea a fines del mes pasado, Smith y los tres matemáticos que lo ayudaron a confirmar el descubrimiento revelaron una nueva forma llamada "el espectro".

No requiere una imagen especular, lo que lo convierte en un einstein aún más puro.

Craig Kaplan, un científico informático de la Universidad de Waterloo en Canadá, dijo a AFP que era "una historia divertida y casi ridícula, pero maravillosa".

Dijo que Smith, un técnico retirado de impresión que vive en East Riding de Yorkshire, le envió un correo electrónico "de la nada" en noviembre.

Smith había encontrado algo "que no se comportaba de acuerdo con sus expectativas normales sobre cómo se comportan las formas", dijo Kaplan.

Si se colocan varias de estas formas de cartón juntas en una mesa, se puede seguir construyendo hacia afuera sin que se establezca un patrón regular.

Usando programas informáticos, Kaplan y otros dos matemáticos demostraron que la forma seguía haciendo esto en un plano infinito, convirtiéndose en el primer einstein o "monotil aperiódico".

Cuando publicaron su primer preimpreso en marzo, entre los inspirados estaba Yoshiaki Araki. El entusiasta japonés de la tiling hizo arte usando el sombrero y otra forma aperiódica creada por el equipo llamada "la tortuga", a veces usando versiones volteadas.

Smith se inspiró y comenzó a explorar formas de evitar la necesidad de voltear su sombrero.

Menos de una semana después de publicar su primer documento, Smith le envió un nuevo formulario por correo electrónico a Kaplan.

Al principio, Kaplan se negó a creerlo. "No hay forma de que sea tan fácil", dijo.

Pero el análisis confirmó que la "pieza (1,1)" era un "einestein no reflectante", dijo.

Algo todavía les molestaba: aunque esta pieza podría continuar para siempre sin repetir un patrón, esto requería una "prohibición artificial" contra el uso de una forma volteada, dijo.

Así que añadieron pequeñas muescas o curvas a los bordes, asegurándose de que solo se pudiera usar la versión no volteada para crear "el espectro".

Kaplan dijo que ambos documentos fueron enviados a revistas revisadas por pares. Pero el mundo de las matemáticas no esperó para expresar su asombro.

Marjorie Senechal, una matemática del Smith College de Estados Unidos, dijo a AFP que los descubrimientos eran "emocionantes, sorprendentes y asombrosos".

Dijo que espera que el espectro y sus parientes "lleven a una comprensión más profunda del orden en la naturaleza y la naturaleza del orden".

Doris Schattschneider, una matemática del Moravian College en Estados Unidos, dijo que ambas formas eran "impresionantes".

Incluso el matemático ganador del Nobel Roger Penrose, cuyo mejor esfuerzo anterior había limitado el número de baldosas aperiódicas a dos en la década de 1970, no estaba seguro de que algo así fuera posible, dijo Schattschneider.

Penrose, de 91 años, estará entre quienes celebrarán las nuevas formas durante el evento de dos días "Hatfest" en la Universidad de Oxford el próximo mes.

Todos los involucrados expresaron asombro de que la idea fuera lograda por alguien sin formación en matemáticas.

"La respuesta cayó del cielo y en las manos de un aficionado, y lo digo en el mejor sentido posible, un amante del tema que lo explora fuera de la práctica profesional", dijo Kaplan.

"Este es el tipo de cosa que no debería suceder, pero muy felizmente para la historia de la ciencia, sucede ocasionalmente, donde un destello nos trae la respuesta de una vez por todas".

© 2023 AFP