New Research Explains Mysteries of Gravitational Wave Collapse

The date of this article is November 15, 2023.

This article has been examined in accordance with the editorial process and policies of Science X. The credibility of the content has been ensured by editors, highlighting the following qualities:

• The content has been fact-checked
• The source is trusted
• The article has been proofread

The author is Ingrid Fadelli from Phys.org

Black holes, the areas of space where the gravitational pull is so dominant that even light cannot escape, remain a significant area of study. Despite countless studies, the physics of their creation is yet to be fully grasped.

Gravitational collapse results in black holes. This process is simply the contraction of an astronomical body caused by its own gravitational pull, which draws matter towards its center. Whether an object undergoing this collapse transforms into a black hole or not is determined by its specific properties.

The critical phenomena result from collapses wherein the object teeters on the brink, undecided if it will become a black hole or not. Physicists have been striving to figure out these critical phenomena for years, as many other known physical systems share some of their traits. Recently, an international team of researchers found correlations between three independently done numerical simulations of these phenomena, aiding in solving persistent puzzles in this field of study.

The phenomena of critical gravitational collapse were first reported approximately 30 years ago by Matt Choptuik, according to Thomas W. Baumgarte, a co-author of the paper. This gained the attention of many researchers due to its shared properties with critical phenomena in other domains of physics.

The critical collapse properties include universality and self-similarity. Universality implies that the solution will consistently be the same as the onset of a black hole's formation nears, regardless of how a calculation commences. Self-similarity suggests that this universal answer will replicate the same patterns as the physical scale lowers.

Baumgarte elaborated that prior calculations involved a scalar field while similar effects for gravitational collapse of gravitational waves were later reported by Andrew Abrahams and Chuck Evans. A distinguishing factor was that spherical symmetry was a characteristic of only the former, while the latter lacked it.

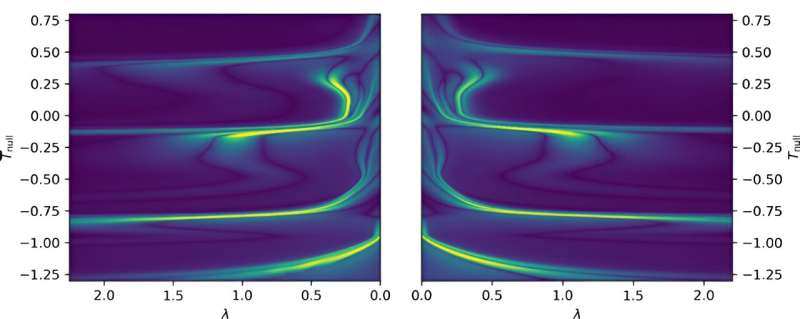
The mystery of critical collapse of pure gravity' has been unresolved for nearly three decades since Abrahams and Evans' results were proven difficult to replicate. However, recently, separate numerical simulations by three research groups utilizing different codes shed light on this matter.

Each of these codes factors in Einstein's equations of general relativity but employs different numerical strategies such as spectral methods versus finite-difference methods,' Baumgarte further explained. All three also adopted different rates at which time advances in the codes. The core objective of their recent study was to examine the recently conducted numerical simulations and bridge the independent research efforts, thereby gaining further insights into gravitational collapse.

'As a first finding we report that, despite all the numerical differences, our codes produce completely consistent results for the critical collapse of gravitational waves,' Baumgarte said. ' This gives us confidence that these findings are correct, and not numerical artifacts. Making a suitable choice for the slicing condition turns out to be crucial: a very common other choice, one that has been successful for many other numerical relativity simulations, fails for this case, which explains why some previous attempts to solve this problem failed.'

Notably, in their three independent numerical simulations, the researchers found no evidence supporting the property of universality. In other words, they found that starting the numerical with different initial data resulted in different values while approaching the formation of a black hole.

'Our findings explain another piece of the puzzle,' Baumgarte said. 'Some previous studies had reported differences from the results of Abrahams and Evans, which therefore appeared conflicting, However, those studies also used different initial data. A disagreement between the results therefore constitutes a contradiction only under the assumption of universality—for which we do not see any evidence.'

While the researchers found no evidence of universality, they found approximate evidence of self-similarity. Interestingly, however, unlike that observed in the case of critical collapse in spherical symmetry, the self-similarity they observed did not appear to be exact.

Back in the 1990s, Abrahams and Evans had also reported a non-exact self-similarity. These recent results are thus aligned with previous findings, potentially suggesting that reported departures from an exact self-similarity could be linked to the absence of a spherical symmetry.

The recent work by Baumgarte and his colleagues could soon pave the way for new numerical and theoretical studies aimed at further studying and re-framing the critical collapse of gravitational waves. This could bring physicists closer to unveiling the nature and mysteries of this intriguing physical phenomenon, known to precede the formation of black holes.

'While we believe that our work has resolved several open questions in the context of critical collapse of gravitational waves, several follow-up questions remain,' Baumgarte added. 'For example, we found approximately self-similar solutions for some families of initial data, but not for others, and the nature of the 'threshold solution' for those other families remains unclear.

'It would also be desirable to perform simulations with better fine-tuning to the onset of black-hole formation (e.g., using numerical codes with better resolution and/or other improvements) to explore whether a universal critical solution emerges for fine-tuning that is better than anybody has achieved so far.

'Finally, we plan to investigate what causes the departures from an exact self-similarity and determine if these departures are directly related to the absence of spherical symmetry.'

© 2023 Science X Network